Note
Go to the end to download the full example code.
O-information and its derivatives for network behavior and encoding#
This example illustrates how to use the O-information and how it’s linked to other metrics such as the Total Correlation (TC), the Dual Total Correlation (DTC), the S-Information and the gradient O-information. We recommend reading Rosas et al. 2019 [24].
import matplotlib.pyplot as plt
import numpy as np
from hoi.metrics import DTC, TC, GradientOinfo, Oinfo, Sinfo
from hoi.utils import get_nbest_mult
plt.style.use("ggplot")
Data simulation#
Let’s first simulate some data to showcase the different metrics. Here, we are going to simulate a network of 6 nodes, then we introduce redundancy between nodes (0, 1, 2) and synergy between nodes (3, 4, 5). For further information about how to simulate redundant and synergistic interactions, checkout the example How to simulate redundancy and synergy
# network of 6 nodes and 1000 samples each
x = np.random.rand(1000, 6)
# inject redundancy between nodes (0, 1, 2)
x[:, 1] += x[:, 0]
x[:, 2] += x[:, 0]
# inject synergy between nodes (3, 4, 5)
x[:, 3] += x[:, 4] + x[:, 5]
O-information for network behavior#
The O-information is a multivariate measure of information capable of disentangling whether a subset of a variable X tend to have synergistic or redundant interactions. The O-information is defined as the difference between two quantities, the Total Correlation (TC) and Dual Total Correlation (DTC).
Total Correlation (TC)#
The TC is defined as :
To give an intuition about the TC, the \(\sum_{j=1}^{n} H(X_{j})\) quantifies the amount of information carried by individual nodes in a system while \(H(X^{n})\) also contains the information carried by individual node plus their interactions. Then, by taking the subtraction between the two quantities we isolate the information contains in the interactions. That’s why the TC quantifies the strength of the “collective constraints” which is related to redundancy.
# compute hoi using TC :
model = TC(x)
hoi = model.fit(method="gc", minsize=3, maxsize=3)
# get the multiplets with largest values of hoi
print(get_nbest_mult(hoi, model))
0%| | 0/1 [00:00<?, ?it/s]
100%|██████████| TC (3): 1/1 [00:00<00:00, 3.61it/s]
index order hoi multiplet
0 0 3 0.948907 [0, 1, 2]
1 19 3 0.646319 [3, 4, 5]
2 4 3 0.486022 [0, 2, 3]
3 5 3 0.485621 [0, 2, 4]
4 6 3 0.484230 [0, 2, 5]
As we can see from the table above, the TC found the multiplet (0, 1, 2), defined as a redundant triplet with the largest value.
Dual Total Correlation (DTC)#
The DTC is defined as :
Again, the DTC is also defined as the difference between two terms. The first one, \(H(X^{n})\), just as in the TC, quantifies the amount of information of the whole system (i.e. the information of individual nodes and their interactions). To this quantity, we subtract the term \(\sum_{j=1}^{n} H(X_j|X_{-j}^{n})\) which represents the sum of information of individual nodes (\(\sum_{j=1}^{n} H(X_j)\)) to which we remove the influence of all other nodes except the one concerned (\(|X_{-j}^{n}\)). Said differently, this conditioning allows to isolate the intrinsic entropy of each node \(X_{j}\) that is not shared with others. Consequently, this difference isolates the “shared randomness” which is linked to the synergy.
# compute hoi using DTC :
model = DTC(x)
hoi = model.fit(method="gc", minsize=3, maxsize=3)
# get the multiplets with largest values of hoi
print(get_nbest_mult(hoi, model))
0%| | 0/1 [00:00<?, ?it/s]
100%|██████████| DTC (3): 1/1 [00:00<00:00, 6.70it/s]
index order hoi multiplet
0 19 3 0.824267 [3, 4, 5]
1 0 3 0.749583 [0, 1, 2]
2 4 3 0.485729 [0, 2, 3]
3 5 3 0.485553 [0, 2, 4]
4 6 3 0.484223 [0, 2, 5]
This time, the DTC finds the triplet (3, 4, 5) as the one with the largest value of HOI and it’s normal because this triplet is synergistic and the DTC is related to synergy.
O-information#
Finally, the O-information is defined as the difference between the TC and DTC. As both quantities are respectively linked to redundancy and synergy, the O-information is going to be positive when a system is dominated by redundant interactions and negative when the system is dominated by synergistic interactions. The mathematical definition of the O-information is given by :
# compute hoi using the O-information :
model = Oinfo(x)
hoi = model.fit(method="gc", minsize=3, maxsize=3)
# get the multiplets with largest values of hoi
print(get_nbest_mult(hoi, model))
0%| | 0/1 [00:00<?, ?it/s]
100%|██████████| Oinfo (3): 1/1 [00:00<00:00, 6.01it/s]
index order hoi multiplet
0 0 3 0.199325 [0, 1, 2]
1 4 3 0.000292 [0, 2, 3]
2 5 3 0.000068 [0, 2, 4]
3 9 3 0.000012 [0, 4, 5]
4 6 3 0.000008 [0, 2, 5]
5 3 3 -0.000539 [0, 1, 5]
6 2 3 -0.001514 [0, 1, 4]
7 16 3 -0.001626 [2, 3, 4]
8 7 3 -0.001666 [0, 3, 4]
9 19 3 -0.177948 [3, 4, 5]
Finally, the O-information isolates the triplet (0, 1, 2) as the one with the largest positive, redundant, hoi and the triplet (3, 4, 5) as the one with the smallest, negative and therefore synergistic multiplet.
S-information#
Finally, the S-information is defined as the sum of the TC and DTC :
# compute hoi using the S-information :
model = Sinfo(x)
hoi = model.fit(method="gc", minsize=3, maxsize=3)
# get the multiplets with largest values of hoi
print(get_nbest_mult(hoi, model))
0%| | 0/1 [00:00<?, ?it/s]
100%|██████████| Sinfo (3): 1/1 [00:00<00:00, 5.81it/s]
index order hoi multiplet
0 0 3 1.698491 [0, 1, 2]
1 19 3 1.470587 [3, 4, 5]
2 4 3 0.971751 [0, 2, 3]
3 5 3 0.971174 [0, 2, 4]
4 6 3 0.968453 [0, 2, 5]
The S-info isolates the two triplets (0, 1, 2) and (3, 4, 5), even if both have different characters (redundant and synergistic)
O-information for network encoding#
The previous section focused on network behavior, i.e. characterizing the type of interactions between the elements of a system. But what if we want now to add a target variable, i.e. ask the question whether a multiplet is carrying redundant or synergistic information about a target variable \(Y\). Intuitively, we could quantify the difference between the information carried by all of the nodes \(X_{j}\) with target minus the information of all of the nodes without the target. This is the idea behind the gradient O-information, defined as the difference between the two O-information :
Simulating redundant encoding#
To simulate redundant encoding, we send a copy of \(Y\) to the nodes (0, 1, 2)
# network of 6 nodes and 1000 samples each
x = np.random.rand(1000, 6)
# target variable
y = np.random.rand(1000)
# redundancy between nodes (0, 1, 2) about y
x[:, 0] += y
x[:, 1] += y
x[:, 2] += y
# compute gradient o-info :
model = GradientOinfo(x, y)
hoi = model.fit(method="gc", minsize=3, maxsize=3)
# get the multiplets with largest values of hoi
print(get_nbest_mult(hoi, model, n_best=3))
0%| | 0/1 [00:00<?, ?it/s]
100%|██████████| Oinfo (3): 1/1 [00:00<00:00, 5.81it/s]
0%| | 0/1 [00:00<?, ?it/s]
100%|██████████| Oinfo (3): 1/1 [00:00<00:00, 4.52it/s]
index order hoi multiplet
0 0 3 0.387099 [0, 1, 2]
1 3 3 0.241662 [0, 1, 5]
2 2 3 0.241096 [0, 1, 4]
3 14 3 -0.001188 [1, 3, 5]
4 8 3 -0.001462 [0, 3, 5]
5 7 3 -0.002715 [0, 3, 4]
The gradient O-info retrieved redundant interactions between nodes (0, 1, 2) about \(Y\)
Simulating synergistic encoding#
To simulate synergistic encoding, \(Y\) is going to be defined as the sum between nodes (3, 4, 5)
# network of 6 nodes and 1000 samples each
x = np.random.rand(1000, 6)
# synergy between nodes (3, 4, 5) about y
y = x[:, 3] + x[:, 4] + x[:, 5]
# compute gradient o-info :
model = GradientOinfo(x, y)
hoi = model.fit(method="gc", minsize=3, maxsize=3)
# get the multiplets with largest values of hoi
print(get_nbest_mult(hoi, model, n_best=3))
0%| | 0/1 [00:00<?, ?it/s]
100%|██████████| Oinfo (3): 1/1 [00:00<00:00, 5.42it/s]
0%| | 0/1 [00:00<?, ?it/s]
100%|██████████| Oinfo (3): 1/1 [00:00<00:00, 5.28it/s]
index order hoi multiplet
0 3 3 0.002728 [0, 1, 5]
1 2 3 0.002610 [0, 1, 4]
2 11 3 0.001531 [1, 2, 4]
3 13 3 -0.179843 [1, 3, 4]
4 16 3 -0.180912 [2, 3, 4]
5 19 3 -2.347114 [3, 4, 5]
The gradient O-info retrieved synergistic interactions between nodes (3, 4, 5) about \(Y\)
Combining redundant and synergistic codings using a multivariate target#
# network of 6 nodes and 1000 samples each
x = np.random.rand(1000, 6)
# define a bivariate target variable
y = np.random.rand(1000, 2)
# redundancy between nodes (0, 1, 2) about the first column of y
x[:, 0] += y[:, 0]
x[:, 1] += y[:, 0]
x[:, 2] += y[:, 0]
# synergy between nodes (3, 4, 5) about the second column of y
y[:, 1] += x[:, 3] + x[:, 4] + x[:, 5]
# compute gradient o-info :
model = GradientOinfo(x, y)
hoi = model.fit(method="gc", minsize=3, maxsize=3)
# get the multiplets with largest values of hoi
print(get_nbest_mult(hoi, model, n_best=3))
0%| | 0/1 [00:00<?, ?it/s]
100%|██████████| Oinfo (3): 1/1 [00:00<00:00, 5.68it/s]
0%| | 0/1 [00:00<?, ?it/s]
100%|██████████| Oinfo (3): 1/1 [00:00<00:00, 4.13it/s]
index order hoi multiplet
0 0 3 0.371283 [0, 1, 2]
1 2 3 0.214285 [0, 1, 4]
2 3 3 0.214246 [0, 1, 5]
3 13 3 -0.090281 [1, 3, 4]
4 16 3 -0.092041 [2, 3, 4]
5 19 3 -0.397403 [3, 4, 5]
The gradient O-info retrieved the redundant interactions between (0, 1, 2) and synergistic interactions between (3, 4, 5) about \(Y\).
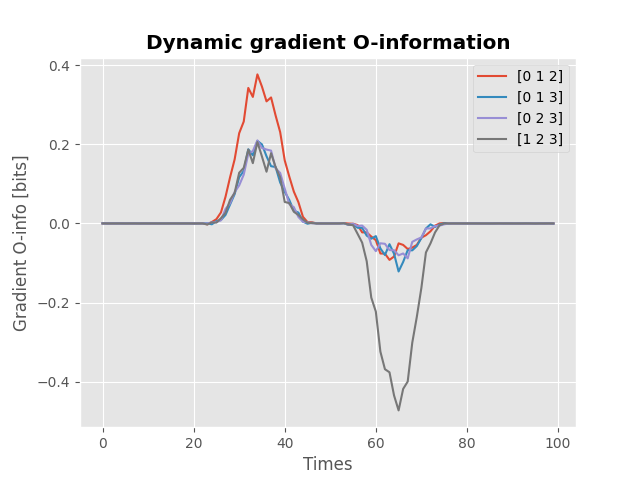
Dynamic redundant and synergistic codings#
Finally, we can compute the O-information and Gradient O-information on dynamic data
# network of 6 nodes, 1000 samples each and a 100 time points
x = np.random.rand(1000, 4, 100)
# define a dynamic target variable
y = np.random.rand(1000, 1, 100)
# define a hanning window
win = np.hanning(30)
# redundancy between nodes (0, 1, 2) about :math:`Y` between samples [20, 50]
x[:, 0, 20:50] += y[:, 0, 20:50] * win
x[:, 1, 20:50] += y[:, 0, 20:50] * win
x[:, 2, 20:50] += y[:, 0, 20:50] * win
# synergy between nodes (1, 2, 3) about :math:`Y` between samples [50, 80]
y[:, 0, 50:80] += (x[:, 1, 50:80] + x[:, 2, 50:80] + x[:, 3, 50:80]) * win
model = GradientOinfo(x, y)
hoi = model.fit(method="gc", minsize=3, maxsize=3)
for n_m, m in enumerate(model.multiplets):
plt.plot(hoi[n_m], label=str(m))
plt.xlabel("Times")
plt.ylabel("Gradient O-info [bits]")
plt.title("Dynamic gradient O-information", fontweight="bold")
plt.legend()
plt.show()
0%| | 0/1 [00:00<?, ?it/s]
100%|██████████| Oinfo (3): 1/1 [00:00<00:00, 2.72it/s]
0%| | 0/1 [00:00<?, ?it/s]
100%|██████████| Oinfo (3): 1/1 [00:00<00:00, 3.54it/s]
Total running time of the script: (0 minutes 3.242 seconds)
