Theoretical background#
Since the seminal work of Claude Shannon [28], in the second half of the 20th century, Information Theory (IT) has been proven to be an invaluable framework to decipher the intricate web of interactions underlying a broad range of different complex systems [37]. In this line of research, a plethora of approaches has been developed to investigate relationships between pairs of variables, shedding light on many properties of complex systems in a vast range of different fields. However, a growing body of literature has recently highlighted that investigating the interactions between groups of more than 2 units, i.e. Higher Order Interactions (HOI), allows to unveil effects that can be neglected by pairwise approaches [3]. Hence, how to study HOI has became a more and more important question in recent times [2]. In this context, new approaches based on IT emerged to investigate HOI in terms of information content; more into details, different metrics have been developed to estimate from the activity patterns of a set of variables, whether or not they are interacting and which kind of interaction they present [33, 36].
These metrics are particularly relevant in situations where data about the interactions between the units of a complex system is unavailable, and only their activity is observable. In this context, the study of higher-order information content enables the investigation of higher-order interactions within the system. For instance, in neuroscience, while it’s often possible to record the activity of different brain regions, clear data on their interactions is lacking and multivariate statistical analysis, as higher-order information, allows to investigate the interactions between different brain regions. It has to be noted that this approaches are based on the study of statistical effects among data and can not directly target structural or mechanistic interactions [23].
Most of the information metrics implemented are based on the concepts of Synergy and Redundancy, formalized in terms of IT by the Partial Information Decomposition (PID) framework [38]. Even though these metrics are theoretically well defined, when concretely using them to study and computing the higher-order structure of a system, two main problems come into play: how to estimate entropies and information from limited data set, with different hypothesis and characteristics, and how to handle the computational cost of such operations. In our work we provided a complete set of estimators to deal with different kinds of data sets, e.g. continuous or discrete, and we used the python library Jax to deal with the high computational cost. In the following part we will introduce the information theoretical tools necessary to understand and use the metrics developed in this toolbox. Then we will present quickly the theory behind the metrics developed, their use and possible interpretation. Finally, we are going to discuss limitations and future developments of our work.
Core information theoretic measures#
In this section, we delve into some fundamental information theoretic measures, such as Shannon Entropy and Mutual Information (MI), and their applications in the study of pairwise interactions. Besides the fact that these measures play a crucial role in various fields such as data science and machine learning, as we will see in the following parts, they serve as the building blocks for quantifying information and interactions between variables at higher-orders.
Measuring Entropy#
Shannon entropy is a fundamental concept in IT, representing the amount of uncertainty or disorder in a random variable [28]. Its standard definition for a discrete random variable \(X\), with probability mass function \(P(X)\), is given by:
However, estimating the probability distribution \(P(X)\) from data can be challenging. When dealing with a discrete variable that takes values from a limited set \({x_{1}, x_{2}, ...}\), one can estimate the probability distribution by computing the frequencies of each state \(x_{i}\). In this scenario we estimate the probability \(P(X=x_{i}) = n_{i}/N\), where \(n_{i}\) is the number of occurrences \(X=x_{i}\) and \(N\) is the number of data points. This can present problems due to size effects when using a small data set and variables exploring a big set of states.
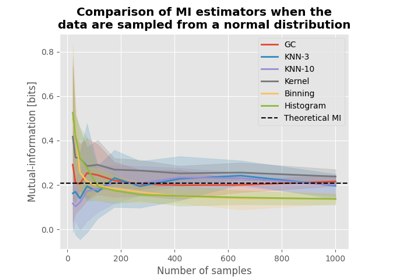
A more complicated and common scenario is the one of continuous variables. To estimate the entropy of a continuous variable, different methods are implemented in the toolbox:
Histogram estimator, that consists in binning the continuous data in a discrete set of bins. In this way, variables are discretized and the entropy can be computed as described above, correcting for the bin size .
Binning method, that allow to estimate the entropy of a discrete variable estimating the probability of each possible values in a frequentist approach. Note that this procedure can be performed also on continuous variables after binarization in many different ways [7, 8, 9].
K-Nearest Neighbors (KNN), that estimates the probability distribution by considering the K-nearest neighbors of each data point [15].
Kernel Density Estimation that uses kernel functions to estimate the probability density function, offering a smooth approximation [20].
The parametric estimation, that is used when the data is gaussian and allows to compute the entropy as a function of the variance [11, 13].
Note that all the functions mentioned in the following part are based on the computation of entropies, hence we advise care in the choice of the estimator to use.
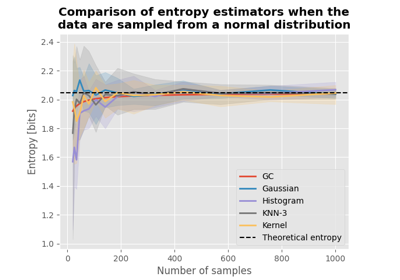
Comparison of entropy estimators for various distributions
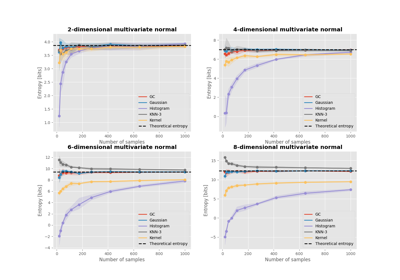
Comparison of entropy estimators for a multivariate normal
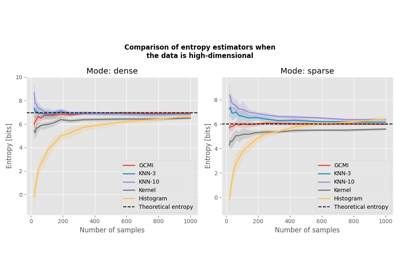
Comparison of entropy estimators with high-dimensional data

Introduction to core information theoretical metrics
Measuring Mutual Information (MI)#
One of the most used functions in the study of pairwise interaction is the Mutual Information (MI) that quantifies the statistical dependence or information shared between two random variables [28, 37]. It is defined mathematically using the concept of entropies. For two random variables X and Y, MI is given by:
Where:
\(H(X)\) and \(H(Y)\) are the entropies of individual variables \(X\) and \(Y\). \(H(X,Y)\) is the joint entropy of \(X\) and \(Y\). MI between two variables, quantifies how much knowing one variable reduces the uncertainty about the other and measures the interdependency between the two variables. If they are independent, we have \(H(X,Y)=H(X)+H(Y)\), hence \(MI(X,Y)=0\). Since the MI can be reduced to a signed sum of entropies, the problem of how to estimate MI from continuous data can be reduced to the problem, discussed above, of how to estimate entropies. An estimator that has been recently developed and presents interesting properties when computing the MI is the Gaussian Copula estimator [13]. This estimator is based on the statistical theory of copulas and is proven to provide a lower bound to the real value of MI, this is one of its main advantages: when computing MI, Gaussian copula estimator avoids false positives. Play attention to the fact that this can be mainly used to investigate relationships between two variables that are monotonic.
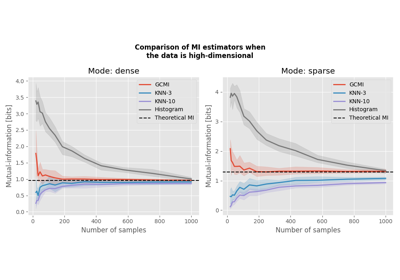
Comparison of MI estimators with high-dimensional data

Introduction to core information theoretical metrics
From pairwise to higher-order interactions#
The information theoretic metrics involved in this work are all based in principle on the concept of Shannon entropy and mutual information. Given a set of variables, a common approach to investigate their interaction is by comparing the entropy and the information of the joint probability distribution of the whole set with the entropy and information of different subsets. This can be done in many different ways, unveiling different aspects of HOI [33, 36]. The metrics implemented in the toolbox can be divided in two main categories:
Network behavior category containing metrics that quantify collective higher-order
behaviors from multivariate data. These information theoretical measures quantify the degree of higher-order functional interactions between different variables.
Network encoding category containing measures that quantify the information carried
by higher-order functional interactions about a set of external target variables.
In the following parts we are going through all the metrics that have been developed in the toolbox, providing some insights about their theoretical foundation and possible interpretations.
Network behavior#
The metrics that are listed in this section quantify collective higher-order behaviors from multivariate data. Information-theoretic measures, such as Total Correlation and O-information, are useful for studying the collective behavior of three or more components in complex systems, such as brain regions, economic indicators or psychological variables. Once data is gathered, these network behavior measures can be applied to unveil new insights about the functional interactions characterizing the system under study. In this section, we list all the metrics of network behavior, that are implemented in the toolbox, providing a concise explanation and relevant references.
Total correlation#
Total correlation, hoi.metrics.TC, is the oldest extension of mutual information to
an arbitrary number of variables [29, 37].
For a group of variables \(X^n = \{ X_1, X_2, ..., X_n \}\), it is defined in the following way:
The total correlation quantifies the strength of collective constraints ruling the systems, it is sensitive to information shared between single variables and it can be associated with redundancy.
O-information and its derivatives for network behavior and encoding
Dual Total correlation#
Dual total correlation, hoi.metrics.DTC, is another extension of mutual information to
an arbitrary number of variables, also known as binding information and excess
entropy, [30]. It quantifies the part of the joint entropy that
is shared by at least two or more variables in the following way:
Where \(X_{-j}^n\) is the set of all the variables in \(X^n\) apart from \(X_j\), \(X_{-j}^{n}= \{ X_1, X_2, ..., X_{j-1}, X_{j+1}, ..., X_n \}\), so that \(H(X_j|X_{-j}^{n})\) is the entropy of \(X_j\) not shared by any other variable. This measure is higher in systems in which lower order constraints prevails.

O-information and its derivatives for network behavior and encoding
S information#
The S-information (also called exogenous information), hoi.metrics.Sinfo, is defined
as the sum between the total correlation (TC) plus the dual total
correlation (DTC), [14]:
It is sensitive to both redundancy and synergy, quantifying the total amount of constraints ruling the system under study.

O-information and its derivatives for network behavior and encoding
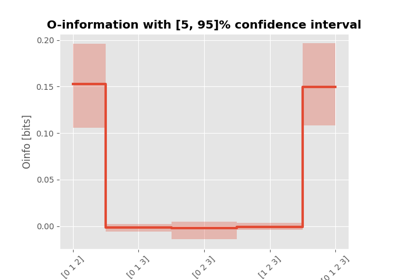
O-information#
One prominent metric that has emerged in the pursuit of higher-order understanding is the
O-information, hoi.metrics.Oinfo. Introduced by Rosas in 2019 [24],
O-information elegantly addresses the challenge of quantifying higher-order dependencies by
extending the concept of mutual information. Given a multiplet of \(n\) variables,
\(X^n = \{ X_1, X_2, …, X_n \}\), its formal definition is the following:
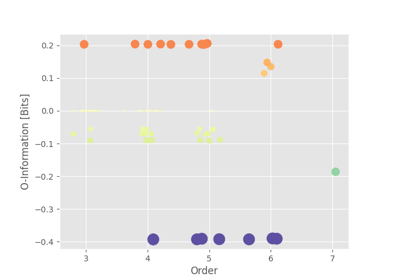
Where \(X_{-j}^n\) is the set of all the variables in \(X^n\) apart from \(X_j\). The O-information can be written also as the difference between the total correlation and the dual total correlation and it is shown to be a proxy of the difference between redundancy and synergy: when the O-information of a set of variables is positive this indicates redundancy, when it is negative, synergy. In particular when working with big data sets it can become complicated

O-information and its derivatives for network behavior and encoding
Topological information#
The topological information (TI), hoi.metrics.InfoTopo, a generalization of the
mutual information to higher-order has been introduced and presented to
test uniformity and dependence in the data [4]. Its formal
definition for a set of variables \(X^n\), is the following:
- Note that for a set of two variables, \(TI(X,Y) = MI(X,Y)\) and that for a set of three variables,
\(TI(X,Y,Z)=\Omega(X,Y,Z)\). As the
O-information this function can be interpreted in terms of redundancy and synergy, more into details when it is positive it indicates that the system is dominated by redundancy, when it is negative, synergy.
The Integrated Information Decomposition#
Recently it has been drawn a lot of attention by different metrics focusing on decomposing the information that two variables carry about their own future [18]. A new decomposition of the information dynamics have been developed to achieve a more nuanced description of the temporal evolution of the synergy and the redundancy between different variables. The synergy that is carried by two variables about their joint future, has been associated with the concept of emergence and integration of information [17, 19, 22]. Instead the redundancy that is preserved, often refered too as “double redundancy” [18], has been associated with the concept of robustness, in the sense that it refers to situation in which information is available in different sources, making the evolution process less vulnerable by the lost of elements [17]. It provides already many results in simulated complex systems or in different studies within the field of neuroscience [16, 22]. In our toolbox, it is possible to compute any atoms of the Integrated Information Decomposition (IphiD) [18], using the function:
This function allow to compute the atoms of interest of the integrated information decomposition
framework (phiID). The redundancy is estimated using the approximation of
Minimum Mutual Information (MMI) [1],
in which the redundancy, hoi.metrics.RedundancyphiID, between a couple
of variables \((X, Y)\) is
defined as:
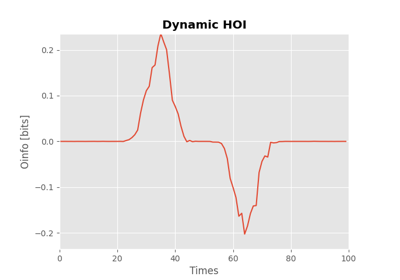
Total dynamical O-information#
The total dynamical O-information, hoi.metrics.dOtot, has been
developed to study the balance between redundancy and synergy in the
context of dynamical systems. This metric provides a comprehensive
framework to analyze the interplay between redundant and synergistic
interactions among a set of variables over time. It is defined as:
Where \(dO_i(X^n)\) can be written as:
Here, \(X_{-j}^n\) represents the set of all variables in \(X^n\) except for \(X_j\), and \(X_{-ij}^n\) is the set excluding both \(X_i\) and \(X_j\). The term \(I(A; B | C)\) denotes the conditional mutual information between variables A and B given C.
Network encoding#
The metrics that are listed in this section focus on measuring the information content that a set of variables carry about an external target of interest. Information-theoretic measures, such as Redundancy-Synergy index and the gradient O-information, are useful for studying the behavior of different variables in relationship with an external target. Once data is gathered, these measures of network encoding can be applied to unveil new insights about the functional interaction modulated by external variables of interest. In this section, we list all the metrics of network encoding, that are implemented in the toolbox, providing a concise explanation and relevant references.
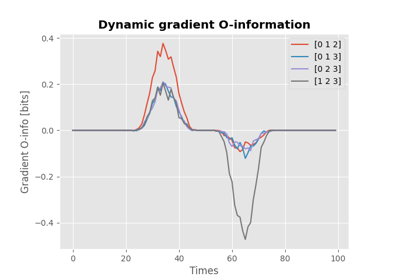
Gradient of O-information#
The O-information gradient, hoi.metrics.GradientOinfo, has been developed to
study the contribution of one or a set of variables to the O-information of the whole
system [25]. In this work we proposed to use this metric
to investigate the relationship between multiplets of source variables and a target
variable. Following the definition of the O-information gradient of order 1, between
the set of variables \(X^n\) and an external target \(Y\) we have:
This metric does not focus on the O-information of a group of variables, instead it reflects the variation of O-information when the target variable is added to the group. This allows to unveil the contribution of the target to the group of variables in terms of O-information, providing insights about the relationship between the target and the group of variables. Note that, when the target is statistically independent from all the variables of the group, the gradient of O-information is 0, when it is greater than 0, the relation between variables and target is characterized by redundancy, when negative, synergy.

O-information and its derivatives for network behavior and encoding
Machine-learning vs. Information theoretic approaches for HOI
Redundancy-Synergy index (RSI)#
Another metric, proposed by Gal Chichek et al in 2001 [5], is the
Redundancy-Synergy index, hoi.metrics.RSI, developed as an extension of mutual
information, aiming to characterize the statistical interdependencies between a group
of variables \(X^n\) and a target variable \(Y\), in terms of redundancy and
synergy, it is computed as:
The RSI is designed to measure directly whether the sum of the information provided separately by all the variables is greater or not with respect to the information provided by the whole group. When RSI is positive, the whole group is more informative than the sum of its parts separately, so the interaction between the variables and the target is dominated by synergy. A negative RSI should instead suggest redundancy among the variables with respect to the target.
Synergy and redundancy (MMI)#
Within the broad research field of IT a growing body of literature has been produced
in the last 20 years about the fascinating concepts of synergy and redundancy. These
concepts are well defined in the framework of Partial Information Decomposition, which
aims to distinguish different “types” of information that a set of sources convey
about a target variable. In this framework, the synergy between a set of variables
refers to the presence of relationships between the target and the whole group that
cannot be seen when considering separately the single parts. Redundancy instead
refers to another phenomena, in which variables contain copies of the same
information about the target. Different definition have been provided in the
last years about these two concepts, in our work we are going to report the
simple case of the Minimum Mutual Information (MMI) [1],
in which the redundancy, hoi.metrics.RedundancyMMI, between a set
of \(n\) variables \(X^n = \{ X_1, \ldots, X_n\}\) and a target \(Y\) is
defined as:
When computing the redundancy in this way the definition
of synergy, hoi.metrics.SynergyMMI, follows:
Where \(X^n_{-i}\) is the set of variables \(X^n\), excluding the variable \(i\). This metric has been proven to be accurate when working with gaussian systems; we advise care when interpreting the results of the redundant interactions, since the definition of redundancy reflects simply the minimum information provided by the source variables.
Bibliography#
Adam B Barrett. Exploration of synergistic and redundant information sharing in static and dynamical gaussian systems. Physical Review E, 91(5):052802, 2015.
Federico Battiston, Enrico Amico, Alain Barrat, Ginestra Bianconi, Guilherme Ferraz de Arruda, Benedetta Franceschiello, Iacopo Iacopini, Sonia Kéfi, Vito Latora, Yamir Moreno, and others. The physics of higher-order interactions in complex systems. Nature Physics, 17(10):1093–1098, 2021.
Federico Battiston, Giulia Cencetti, Iacopo Iacopini, Vito Latora, Maxime Lucas, Alice Patania, Jean-Gabriel Young, and Giovanni Petri. Networks beyond pairwise interactions: structure and dynamics. Physics Reports, 874:1–92, 2020.
Pierre Baudot, Monica Tapia, Daniel Bennequin, and Jean-Marc Goaillard. Topological information data analysis. Entropy. An International and Interdisciplinary Journal of Entropy and Information Studies, 2019. Number: 869. URL: https://www.mdpi.com/1099-4300/21/9/869, doi:10.3390/e21090869.
Gal Chechik, Amir Globerson, M Anderson, E Young, Israel Nelken, and Naftali Tishby. Group redundancy measures reveal redundancy reduction in the auditory pathway. Advances in neural information processing systems, 2001.
Paweł Czyż, Frederic Grabowski, Julia Vogt, Niko Beerenwinkel, and Alexander Marx. Beyond normal: on the evaluation of mutual information estimators. Advances in Neural Information Processing Systems, 2024.
Georges A Darbellay and Igor Vajda. Estimation of the information by an adaptive partitioning of the observation space. IEEE Transactions on Information Theory, 45(4):1315–1321, 1999.
Dominik Endres and Peter Foldiak. Bayesian bin distribution inference and mutual information. IEEE Transactions on Information Theory, 51(11):3766–3779, 2005.
Andrew M Fraser and Harry L Swinney. Independent coordinates for strange attractors from mutual information. Physical review A, 33(2):1134, 1986.
Amir Globerson, Eran Stark, Eilon Vaadia, and Naftali Tishby. The minimum information principle and its application to neural code analysis. Proceedings of the National Academy of Sciences, 106(9):3490–3495, 2009.
Nathaniel R Goodman. Statistical analysis based on a certain multivariate complex gaussian distribution (an introduction). The Annals of mathematical statistics, 34(1):152–177, 1963.
Virgil Griffith and Christof Koch. Quantifying synergistic mutual information. In Guided self-organization: inception, pages 159–190. Springer, 2014.
Robin AA Ince, Bruno L Giordano, Christoph Kayser, Guillaume A Rousselet, Joachim Gross, and Philippe G Schyns. A statistical framework for neuroimaging data analysis based on mutual information estimated via a gaussian copula. Human brain mapping, 38(3):1541–1573, 2017.
Ryan G James, Christopher J Ellison, and James P Crutchfield. Anatomy of a bit: information in a time series observation. Chaos: An Interdisciplinary Journal of Nonlinear Science, 2011.
Alexander Kraskov, Harald Stögbauer, and Peter Grassberger. Estimating mutual information. Physical review E, 69(6):066138, 2004.
Andrea I Luppi, Pedro AM Mediano, Fernando E Rosas, Judith Allanson, John D Pickard, Robin L Carhart-Harris, Guy B Williams, Michael M Craig, Paola Finoia, Adrian M Owen, and others. A synergistic workspace for human consciousness revealed by integrated information decomposition. BioRxiv, pages 2020–11, 2020.
Andrea I Luppi, Fernando E Rosas, Pedro AM Mediano, David K Menon, and Emmanuel A Stamatakis. Information decomposition and the informational architecture of the brain. Trends in Cognitive Sciences, 2024.
Pedro AM Mediano, Fernando E Rosas, Andrea I Luppi, Robin L Carhart-Harris, Daniel Bor, Anil K Seth, and Adam B Barrett. Towards an extended taxonomy of information dynamics via integrated information decomposition. arXiv preprint arXiv:2109.13186, 2021.
Pedro AM Mediano, Fernando E Rosas, Andrea I Luppi, Henrik J Jensen, Anil K Seth, Adam B Barrett, Robin L Carhart-Harris, and Daniel Bor. Greater than the parts: a review of the information decomposition approach to causal emergence. Philosophical Transactions of the Royal Society A, 380(2227):20210246, 2022.
Young-Il Moon, Balaji Rajagopalan, and Upmanu Lall. Estimation of mutual information using kernel density estimators. Physical Review E, 52(3):2318, 1995.
Fernando E Rosas, Pedro AM Mediano, and Michael Gastpar. Characterising directed and undirected metrics of high-order interdependence. arXiv preprint arXiv:2404.07140, 2024.
Fernando E Rosas, Pedro AM Mediano, Henrik J Jensen, Anil K Seth, Adam B Barrett, Robin L Carhart-Harris, and Daniel Bor. Reconciling emergences: an information-theoretic approach to identify causal emergence in multivariate data. PLoS computational biology, 16(12):e1008289, 2020.
Fernando E Rosas, Pedro AM Mediano, Andrea I Luppi, Thomas F Varley, Joseph T Lizier, Sebastiano Stramaglia, Henrik J Jensen, and Daniele Marinazzo. Disentangling high-order mechanisms and high-order behaviours in complex systems. Nature Physics, 18(5):476–477, 2022.
Fernando E. Rosas, Pedro A. M. Mediano, Michael Gastpar, and Henrik J. Jensen. Quantifying high-order interdependencies via multivariate extensions of the mutual information. Physical Review E, 100(3):032305, September 2019. Publisher: American Physical Society. URL: https://link.aps.org/doi/10.1103/PhysRevE.100.032305 (visited on 2022-12-17), doi:10.1103/PhysRevE.100.032305.
Tomas Scagliarini, Davide Nuzzi, Yuri Antonacci, Luca Faes, Fernando E Rosas, Daniele Marinazzo, and Sebastiano Stramaglia. Gradients of o-information: low-order descriptors of high-order dependencies. Physical Review Research, 5(1):013025, 2023.
Elad Schneidman, Susanne Still, Michael J Berry, William Bialek, and others. Network information and connected correlations. Physical review letters, 91(23):238701, 2003.
Thomas Schreiber. Measuring information transfer. Physical Review Letters, 85(2):461–464, 2000.
Claude Elwood Shannon. A mathematical theory of communication. The Bell system technical journal, 27(3):379–423, 1948.
Milan Studen\`y and Jirina Vejnarová. The multiinformation function as a tool for measuring stochastic dependence. Learning in graphical models, pages 261–297, 1998.
TH Sun. Linear dependence structure of the entropy space. Inf Control, 29(4):337–68, 1975.
Mónica Tapia, Pierre Baudot, Christine Formisano-Tréziny, Martial A Dufour, Simone Temporal, Manon Lasserre, Béatrice Marquèze-Pouey, Jean Gabert, Kazuto Kobayashi, and Jean-Marc Goaillard. Neurotransmitter identity and electrophysiological phenotype are genetically coupled in midbrain dopaminergic neurons. Scientific reports, 8(1):13637, 2018.
Han Te Sun. Nonnegative entropy measures of multivariate symmetric correlations. Information and Control, 36:133–156, 1978.
Nicholas Timme, Wesley Alford, Benjamin Flecker, and John M Beggs. Synergy, redundancy, and multivariate information measures: an experimentalist’s perspective. Journal of computational neuroscience, 36:119–140, 2014.
Nicholas Timme, Wesley Alford, Benjamin Flecker, and John M. Beggs. Synergy, redundancy, and multivariate information measures: an experimentalist’s perspective. Journal of computational neuroscience, 36:119–140, 2014.
Nicholas M. Timme and Christopher Lapish. A tutorial for information theory in neuroscience. eNeuro, 2018.
Thomas F Varley. Information theory for complex systems scientists. arXiv preprint arXiv:2304.12482, 2023.
Satosi Watanabe. Information theoretical analysis of multivariate correlation. IBM Journal of research and development, 4(1):66–82, 1960.
Paul L Williams and Randall D Beer. Nonnegative decomposition of multivariate information. arXiv preprint arXiv:1004.2515, 2010.