Bootstrapping and confidence interval

This example illustrates how to estimate the confidence interval around Higher Order Interactions. In addition, it also shows how the bootstrapping can be used to fix the spatial spreading limitation of the O-information. For further information, checkout the example Topological Information : conditioning on orders

import numpy as np

from hoi.metrics import Oinfo
from hoi.plot import plot_landscape
from hoi.utils import get_nbest_mult

from sklearn.utils import resample

import matplotlib.pyplot as plt

plt.style.use("ggplot")

O-information : Redundancy and synergy spread to higher orders

As illustrated in the example Topological Information : conditioning on orders, when using the hoi.metrics.Oinfo, the redundancy define at one order is going to spread across orders. As a reminder, let’s simulate some simple data, a 4-nodes network with 200 samples. For further information about how to simulate redundant and synergistic interactions, checkout the example How to simulate redundancy and synergy

# define the number of samples and nodes in the network
n_samples = 200
n_nodes = 4

# simulate some data
x = np.random.rand(n_samples, n_nodes)

# create redundancy between nodes (0, 1, 2)
x[:, 1] += x[:, 0]
x[:, 2] += x[:, 0]

Now we can estimate the O-information and plot the landscape of hoi

# compute the o-information
model = Oinfo(x, verbose=False)
hoi = model.fit(method="gc", minsize=3)

# plot the landscape
plot_landscape(
    hoi, model=model, kind="scatter", plt_kwargs=dict(cmap="Spectral_r")
)

# also print the hoi with highest values
print(get_nbest_mult(hoi, model=model))

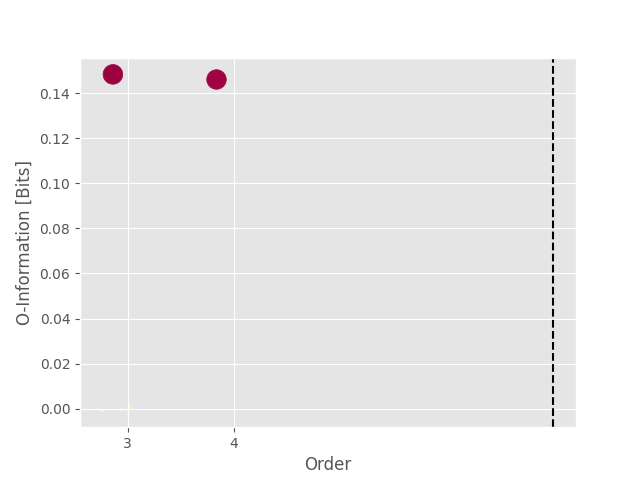
   index  order       hoi     multiplet
0      0      3  0.148361     [0, 1, 2]
1      4      4  0.146471  [0, 1, 2, 3]
2      3      3  0.000526     [1, 2, 3]
3      1      3 -0.000440     [0, 1, 3]
4      2      3 -0.000792     [0, 2, 3]

As we can see from the printed table and the landscape, the highest O-information is achieved for the multiplet (0, 1, 2) at order 3 and the multiplet (0, 1, 2, 3, 4) at order 4. However, we simulated redundancy only between the nodes (0, 1, 2). To fix this with non-parametric statistics, we are going to use bootstrapping to estimate the confidence interval surrounding each estimation of hoi.

Estimation of the confidence interval using a bootstrapping approach

To estimate the confidence interval, we are going to repeat the computations of hoi by randomly sampling the samples. To this end we are going to use the resample method of scikit-learn

Compute bootstrap

Regarding the number of bootstraps, the higher the better but is also more computationally intensive. Here we are going to use 20 to keep the example fast. We recommand at least 200-1000 bootstraps.

# define the number of bootstrap.
n_boots = 20

# define an empty list of hoi
hoi = []

# repeat the computation of hoi `n_boots` times
for n_b in range(20):
    print(f"Bootstrap {n_b + 1} / {n_boots}", end="\r")

    # define a random list of trials
    samples = resample(
        np.arange(n_samples), n_samples=n_samples, random_state=n_b
    )

    # compute the o-info using the subselected trials
    _hoi = model.fit(method="gc", samples=samples, minsize=3).squeeze()

    # append to the list
    hoi.append(_hoi)

# stack the bootstraps over the first dimension
hoi = np.stack(hoi, axis=0)

Bootstrap 1 / 20
Bootstrap 2 / 20
Bootstrap 3 / 20
Bootstrap 4 / 20
Bootstrap 5 / 20
Bootstrap 6 / 20
Bootstrap 7 / 20
Bootstrap 8 / 20
Bootstrap 9 / 20
Bootstrap 10 / 20
Bootstrap 11 / 20
Bootstrap 12 / 20
Bootstrap 13 / 20
Bootstrap 14 / 20
Bootstrap 15 / 20
Bootstrap 16 / 20
Bootstrap 17 / 20
Bootstrap 18 / 20
Bootstrap 19 / 20
Bootstrap 20 / 20

Plot the O-information with the confidence interval

Now we can plot the O-information and its confidence interval.

# compute the mean of the o-information over the bootstraps
hoi_m = hoi.mean(0)

# get the [5, 95]% confidence interval
p_low, p_high = np.percentile(hoi, [5, 95], axis=0)

# plot the results
x_axis = np.arange(hoi_m.shape[0])
ax = plt.step(x_axis, hoi_m, where="mid", lw=3)
plt.fill_between(x_axis, p_low, p_high, alpha=0.3, step="mid")
plt.xticks(x_axis)
plt.gca().set_xticklabels(
    [str(m[0:o]) for m, o in zip(model.multiplets, model.order)], rotation=45
)
plt.xlabel("Multiplet")
plt.ylabel("Oinfo [bits]")
plt.title("O-information with [5, 95]% confidence interval", fontweight="bold")

Text(0.5, 1.0, 'O-information with [5, 95]% confidence interval')

The plot above depicts the average of the O-information over the bootstraps as a bold thick line for all of the multiplets and the shaded area represents the confidence interval. As we can see now, the confidence surrounding the multiplet (0, 1, 2, 3) is not really different from the multiplet (0, 1, 2). Therefore, we can say that the redundancy is mainly carried by the triplet (0, 1, 2) and the addition of the node 3 doesn’t bring much. For comparison, we are going to use the exact same code except that this time, we are going to create redundancy between the quadruplet (0, 1, 2, 3).

# simulate some data
x = np.random.rand(n_samples, n_nodes)

# create redundancy between nodes (0, 1, 2, 3)
x[:, 1] += x[:, 0]
x[:, 2] += x[:, 0]
x[:, 3] += x[:, 0]

# initialize the o-information model
model = Oinfo(x, verbose=False)

# define an empty list of hoi
hoi = []

# repeat the computation of hoi `n_boots` times
for n_b in range(20):
    print(f"Bootstrap {n_b + 1} / {n_boots}", end="\r")

    # define a random list of trials
    samples = resample(
        np.arange(n_samples), n_samples=n_samples, random_state=n_b
    )

    # compute the o-info using the subselected trials
    _hoi = model.fit(method="gc", samples=samples, minsize=3).squeeze()

    # append to the list
    hoi.append(_hoi)

# stack the boostraps over the first dimension
hoi = np.stack(hoi, axis=0)

# compute the mean of the o-information over the bootstraps
hoi_m = hoi.mean(0)

# get the [5, 95]% confidence interval
p_low, p_high = np.percentile(hoi, [5, 95], axis=0)

# plot the results
x_axis = np.arange(hoi_m.shape[0])
ax = plt.step(x_axis, hoi_m, where="mid", lw=3)
plt.fill_between(x_axis, p_low, p_high, alpha=0.3, step="mid")
plt.xticks(x_axis)
plt.gca().set_xticklabels(
    [str(m[0:o]) for m, o in zip(model.multiplets, model.order)], rotation=45
)
plt.xlabel("Multiplet")
plt.ylabel("Oinfo [bits]")
plt.title("O-information with [5, 95]% confidence interval", fontweight="bold")

plt.show()

Bootstrap 1 / 20
Bootstrap 2 / 20
Bootstrap 3 / 20
Bootstrap 4 / 20
Bootstrap 5 / 20
Bootstrap 6 / 20
Bootstrap 7 / 20
Bootstrap 8 / 20
Bootstrap 9 / 20
Bootstrap 10 / 20
Bootstrap 11 / 20
Bootstrap 12 / 20
Bootstrap 13 / 20
Bootstrap 14 / 20
Bootstrap 15 / 20
Bootstrap 16 / 20
Bootstrap 17 / 20
Bootstrap 18 / 20
Bootstrap 19 / 20
Bootstrap 20 / 20

This time, the O-information and confidence interval surrounding the multiplet (0, 1, 2, 3) doesn’t includes the confidence interval of lower order. Therefore we can conclude that the redundancy lies in the quadruplet and not in any of the triplets.

# sphinx_gallery_thumbnail_number = 2