Redundancy-Synergy Index

This example illustrates how to use and interpret the Redundancy-Synergy Index (RSI).

import numpy as np

from hoi.metrics import RSI
from hoi.utils import get_nbest_mult
from hoi.plot import plot_landscape

import matplotlib.pyplot as plt
plt.style.use('ggplot')

Definition

The RSI is a multivariate measure of information capable of disentangling whether a subset of a variable X` carry either redundant or synergistic information about a variable Y. The RSI is defined as :

\[RSI(S; Y) \equiv I(S; Y) - \sum_{x_{i}\in S} I(x_{i}; Y)\]

with :

\[S = x_{1}, ..., x_{n}\]

Positive values of RSI stand for synergy while negative values of RSI reflect redundancy between the X and Y variables.

Simulate univariate redundancy

A very simple way to simulate redundancy is to observe that if a triplet of variables \(X_{1}, X_{2}, X_{3}\) receive a copy of a variable \(Y\), we will observe redundancy between \(X_{1}, X_{2}, X_{3}\) and \(Y\). For further information about how to simulate redundant and synergistic interactions, checkout the example How to simulate redundancy and synergy

# lets start by simulating a variable x with 200 samples and 7 features
x = np.random.rand(200, 7)

# now we can also generate a univariate random variable y
y = np.random.rand(x.shape[0])

# we now send the variable y in the column (1, 3, 5) of x
x[:, 1] += y
x[:, 3] += y
x[:, 5] += y

# define the RSI model and launch it
model = RSI(x, y)
hoi = model.fit(minsize=3, maxsize=5)

# now we can take a look at the multiplets with the highest and lowest values
# of RSI. We will only select the multiplets of size 3 here
df = get_nbest_mult(hoi, model=model, minsize=3, maxsize=3, n_best=3)
print(df)

  0%|          |  0/3 [00:00<?,       ?it/s]
 33%|███▎      | RSI order 3:  1/3 [00:00<00:01,    1.98it/s]
 67%|██████▋   | RSI order 4:  2/3 [00:00<00:00,    2.59it/s]
100%|██████████| RSI order 5:  3/3 [00:01<00:00,    2.78it/s]

   index  order       hoi  multiplet
0      5      3  0.010098  [0, 2, 3]
1     27      3  0.009364  [2, 3, 6]
2     11      3  0.008568  [0, 3, 6]
3     26      3 -0.189541  [2, 3, 5]
4     31      3 -0.193685  [3, 4, 5]
5     20      3 -0.379484  [1, 3, 5]

as you see from the printed table, the multiplet with the lowest (i.e. the most redundant multiplets) is (1, 3, 5).

Simulate multivariate redundancy

In the example above, we simulated a univariate \(Y\) variable (i.e. single column). However, it’s possible to simulate a multivariate variable.

# simulate x again
x = np.random.rand(200, 7)

# simulate a bivariate y variable
y = np.c_[np.random.rand(x.shape[0]), np.random.rand(x.shape[0])]

# we introduce redundancy between the triplet (1, 3, 5) and the first column of
# Y and between (0, 2, 6) and Y
x[:, 1] += y[:, 0]
x[:, 3] += y[:, 0]
x[:, 5] += y[:, 0]
x[:, 0] += y[:, 1]
x[:, 2] += y[:, 1]
x[:, 6] += y[:, 1]

# define the RSI, launch it and inspect the best multiplets
model = RSI(x, y)
hoi = model.fit(minsize=3, maxsize=5)
df = get_nbest_mult(hoi, model=model, minsize=3, maxsize=3, n_best=3)
print(df)

  0%|          |  0/3 [00:00<?,       ?it/s]
 33%|███▎      | RSI order 3:  1/3 [00:00<00:00,    3.26it/s]
 67%|██████▋   | RSI order 4:  2/3 [00:00<00:00,    4.34it/s]
100%|██████████| RSI order 5:  3/3 [00:00<00:00,    4.89it/s]

   index  order       hoi  multiplet
0     11      3 -0.305800  [0, 3, 6]
1      8      3 -0.569149  [0, 2, 6]
2     20      3 -0.573858  [1, 3, 5]

This time, as expected, the two most redundant triplets are (1, 3, 5) and (0, 2, 6)

Simulate univariate and multivariate synergy

Lets move on to the simulation of synergy that is a bit more subtle. One way of simulating synergy is to go the other way of redundancy, meaning we are going to add features of X inside Y. That way, we can only retrieve the Y variable by knowing the subset of X.

# simulate the variable x
x = np.random.rand(200, 7)

# synergy between (0, 3, 5) and 5
y = x[:, 0] + x[:, 3] + x[:, 5]

# define the RSI, launch it and inspect the best multiplets
model = RSI(x, y)
hoi = model.fit(minsize=3, maxsize=5)
df = get_nbest_mult(hoi, model=model, minsize=3, maxsize=3, n_best=3)
print(df)

  0%|          |  0/3 [00:00<?,       ?it/s]
 33%|███▎      | RSI order 3:  1/3 [00:00<00:00,    3.88it/s]
 67%|██████▋   | RSI order 4:  2/3 [00:00<00:00,    5.03it/s]
100%|██████████| RSI order 5:  3/3 [00:00<00:00,    5.59it/s]

   index  order       hoi  multiplet
0     10      3  1.273890  [0, 3, 5]
1     12      3  0.315670  [0, 4, 5]
2     14      3  0.314976  [0, 5, 6]
3     17      3 -0.001248  [1, 2, 5]
4     25      3 -0.001624  [2, 3, 4]
5     15      3 -0.001651  [1, 2, 3]

as we can see here, the highest values of higher-order interactions (i.e. synergy) is achieved for the multiplet (0, 3, 5). Now we can do the same for multivariate synergy

# simulate the variable x
x = np.random.rand(200, 7)

# simulate y and introduce synergy between the subset (0, 3, 5) of x and the
# subset (1, 2, 6)
y = np.c_[x[:, 0] + x[:, 3] + x[:, 5], x[:, 1] + x[:, 2] + x[:, 6]]

# define the RSI, launch it and inspect the best multiplets
model = RSI(x, y)
hoi = model.fit(minsize=3, maxsize=5)
df = get_nbest_mult(hoi, model=model, minsize=3, maxsize=3, n_best=3)
print(df)

  0%|          |  0/3 [00:00<?,       ?it/s]
 33%|███▎      | RSI order 3:  1/3 [00:00<00:00,    3.32it/s]
 67%|██████▋   | RSI order 4:  2/3 [00:00<00:00,    4.46it/s]
100%|██████████| RSI order 5:  3/3 [00:00<00:00,    5.03it/s]

   index  order       hoi  multiplet
0     18      3  1.559214  [1, 2, 6]
1     10      3  1.381920  [0, 3, 5]
2     23      3  0.225347  [1, 4, 6]
3     32      3 -0.001482  [3, 4, 6]

Combining redundancy and synergy

# simulate the variable x and y
x = np.random.rand(200, 7)
y = np.random.rand(200, 2)

# synergy between (0, 1, 2) and the first column of y
y[:, 0] = x[:, 0] + x[:, 1] + x[:, 2]

# redundancy between (3, 4, 5) and the second column of x
x[:, 3] += y[:, 1]
x[:, 4] += y[:, 1]
x[:, 5] += y[:, 1]

# define the RSI, launch it and inspect the best multiplets
model = RSI(x, y)
hoi = model.fit(minsize=3, maxsize=5)
df = get_nbest_mult(hoi, model=model, minsize=3, maxsize=3, n_best=3)
print(df)

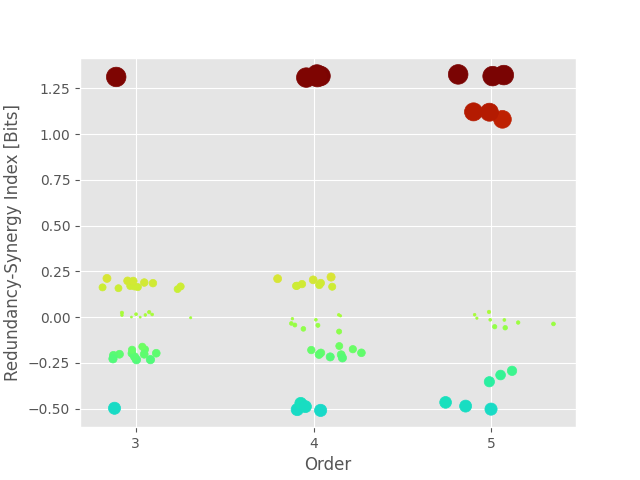
# plot the result at each order to observe the spreading at orders higher than
# 3
plot_landscape(
    hoi,
    model,
    kind="scatter",
    undersampling=False,
    plt_kwargs=dict(cmap="turbo"),
)
plt.show()

  0%|          |  0/3 [00:00<?,       ?it/s]
 33%|███▎      | RSI order 3:  1/3 [00:00<00:00,    3.44it/s]
 67%|██████▋   | RSI order 4:  2/3 [00:00<00:00,    4.63it/s]
100%|██████████| RSI order 5:  3/3 [00:00<00:00,    5.21it/s]

   index  order       hoi  multiplet
0      0      3  1.312485  [0, 1, 2]
1     16      3  0.211186  [1, 2, 4]
2     15      3  0.197775  [1, 2, 3]
3     10      3 -0.232792  [0, 3, 5]
4     20      3 -0.233146  [1, 3, 5]
5     31      3 -0.498634  [3, 4, 5]