Note
Go to the end to download the full example code
Estimate the empirical confidence interval#
This example illustrates how to estimate the confidence interval
import numpy as np
from frites.simulations import sim_local_cc_ms
from frites.dataset import DatasetEphy
from frites.workflow import WfMi
from frites import set_mpl_style
import matplotlib.pyplot as plt
set_mpl_style()
Plotting functions#
First, we define the function that is then going to be used for plotting the results
def plot(mi, pv, ci, color='C0', p=0.05, title='', units='MI (bits)'):
# figure definition
n_cis, n_rois = len(ci['ci']), len(mi['roi'])
width, height = int(np.round(4 * n_rois)), int(np.round(4 * n_cis))
fig, axs = plt.subplots(
nrows=n_cis, ncols=n_rois, sharex=True, sharey=True,
figsize=(width, height))
fig.suptitle(title, fontweight='bold')
# select significant results
mi_s = mi.copy()
mi_s.data[pv.data >= p] = np.nan
# plot the results
for n_r, r in enumerate(mi['roi'].data):
for n_c, c in enumerate(ci['ci'].data):
plt.sca(axs[n_c, n_r])
plt.plot(mi['times'].data, mi.sel(roi=r).data, color='C3',
linestyle='--')
plt.plot(mi['times'].data, mi_s.sel(roi=r).data, color=color, lw=3)
plt.fill_between(
mi['times'].data, ci.sel(ci=c, roi=r, bound='high'),
ci.sel(ci=c, roi=r, bound='low'), alpha=.5, color=color)
plt.title(f"ROI={r}; CI={c}%")
plt.ylabel(units)
Data simulation#
Let’s simulate some data with 10 subjects, 100 epochs per subject and 2 brain regions. As a result, we get a variable x representing the simulated neural data coming from the 10 subjects and y, the task-related variable.
n_subjects, n_epochs, n_roi = 10, 100, 2
x, y, roi, times = sim_local_cc_ms(n_subjects, n_epochs=n_epochs, n_roi=n_roi,
random_state=0)
dt = DatasetEphy(x.copy(), y=y, roi=roi, times=times)
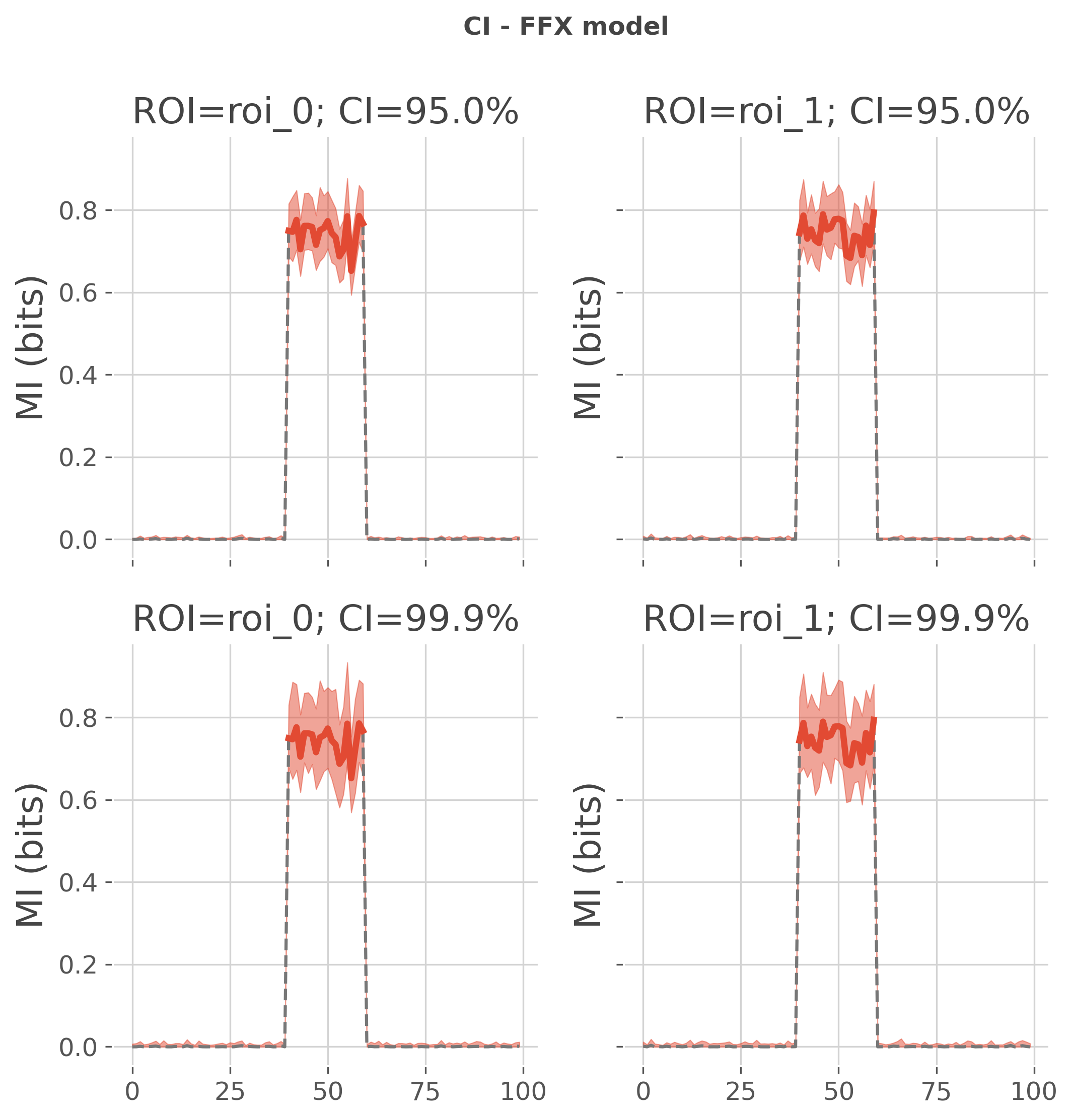
Empirical confidence interval with FFX models#
Then, we estimate the confidence interval when using a fixed-effect model
# computes mi
wf = WfMi(mi_type='cc', inference='ffx')
mi, pv = wf.fit(dt, n_perm=200, n_jobs=1, random_state=0)
# computes confidence interval
ci = wf.confidence_interval(dt, n_boots=200, ci=[95, 99.9], n_jobs=1,
random_state=0)
print(ci)
# plot the results
# sphinx_gallery_thumbnail_number = 1
plot(mi, pv, ci, title='CI - FFX model')
plt.show()
0%| | Estimating MI : 0/2 [00:00<?, ?it/s]
50%|█████ | Estimating MI : 1/2 [00:00<00:00, 3.42it/s]
100%|██████████| Estimating MI : 2/2 [00:00<00:00, 3.50it/s]
100%|██████████| Estimating MI : 2/2 [00:00<00:00, 3.50it/s]
0%| | Estimating CI : 0/2 [00:00<?, ?it/s]
50%|█████ | Estimating CI : 1/2 [00:00<00:00, 2.82it/s]
100%|██████████| Estimating CI : 2/2 [00:00<00:00, 2.82it/s]
100%|██████████| Estimating CI : 2/2 [00:00<00:00, 2.82it/s]
<xarray.DataArray (ci: 2, bound: 2, times: 100, roi: 2)>
array([[[[-7.23073406e-04, -7.16491298e-04],
[-7.22913892e-04, -7.21564212e-04],
[-7.12451612e-04, -3.77852905e-04],
[-7.21695001e-04, -7.23084135e-04],
[-7.20416509e-04, -7.22600946e-04],
[-7.20839755e-04, -7.19997847e-04],
[-7.21475668e-04, -7.16736185e-04],
[-7.21381190e-04, -7.22534403e-04],
[-7.20533649e-04, -7.21103013e-04],
[-7.21385662e-04, -7.19823394e-04],
[-7.23042384e-04, -7.21751861e-04],
[-7.21119570e-04, -7.21950000e-04],
[-7.17653520e-04, -5.43816230e-04],
[-7.22834983e-04, -7.22015522e-04],
[-6.43601312e-04, -7.22082109e-04],
[-7.20890473e-04, -7.01435236e-04],
[-7.21521075e-04, -7.06132196e-04],
[-7.20710467e-04, -7.21843597e-04],
[-7.22542193e-04, -7.21560745e-04],
[-7.22901901e-04, -7.22991019e-04],
...
[ 4.94244866e-03, 1.07339411e-02],
[ 9.79310366e-03, 4.22542676e-03],
[ 6.94442050e-03, 8.52263006e-03],
[ 8.93999326e-03, 1.42579034e-02],
[ 6.89398717e-03, 1.20471159e-02],
[ 1.16844222e-02, 4.71777218e-03],
[ 6.02946251e-03, 5.92530687e-03],
[ 9.03900810e-03, 4.65719321e-03],
[ 1.27212104e-02, 6.39466274e-03],
[ 1.15400850e-02, 1.47285943e-02],
[ 6.34947684e-03, 4.47972739e-03],
[ 4.56949591e-03, 4.61853010e-03],
[ 6.94840438e-03, 4.63257400e-03],
[ 1.17303262e-02, 9.08010769e-03],
[ 4.93415462e-03, 1.25797414e-02],
[ 9.11222803e-03, 6.01635745e-03],
[ 6.81227519e-03, 1.18603074e-02],
[ 5.50806255e-03, 1.50310924e-02],
[ 9.75895521e-03, 1.13908156e-02],
[ 1.10290457e-02, 7.38632124e-03]]]])
Coordinates:
* ci (ci) float64 95.0 99.9
* bound (bound) <U4 'low' 'high'
* times (times) int64 0 1 2 3 4 5 6 7 8 9 ... 90 91 92 93 94 95 96 97 98 99
* roi (roi) <U5 'roi_0' 'roi_1'
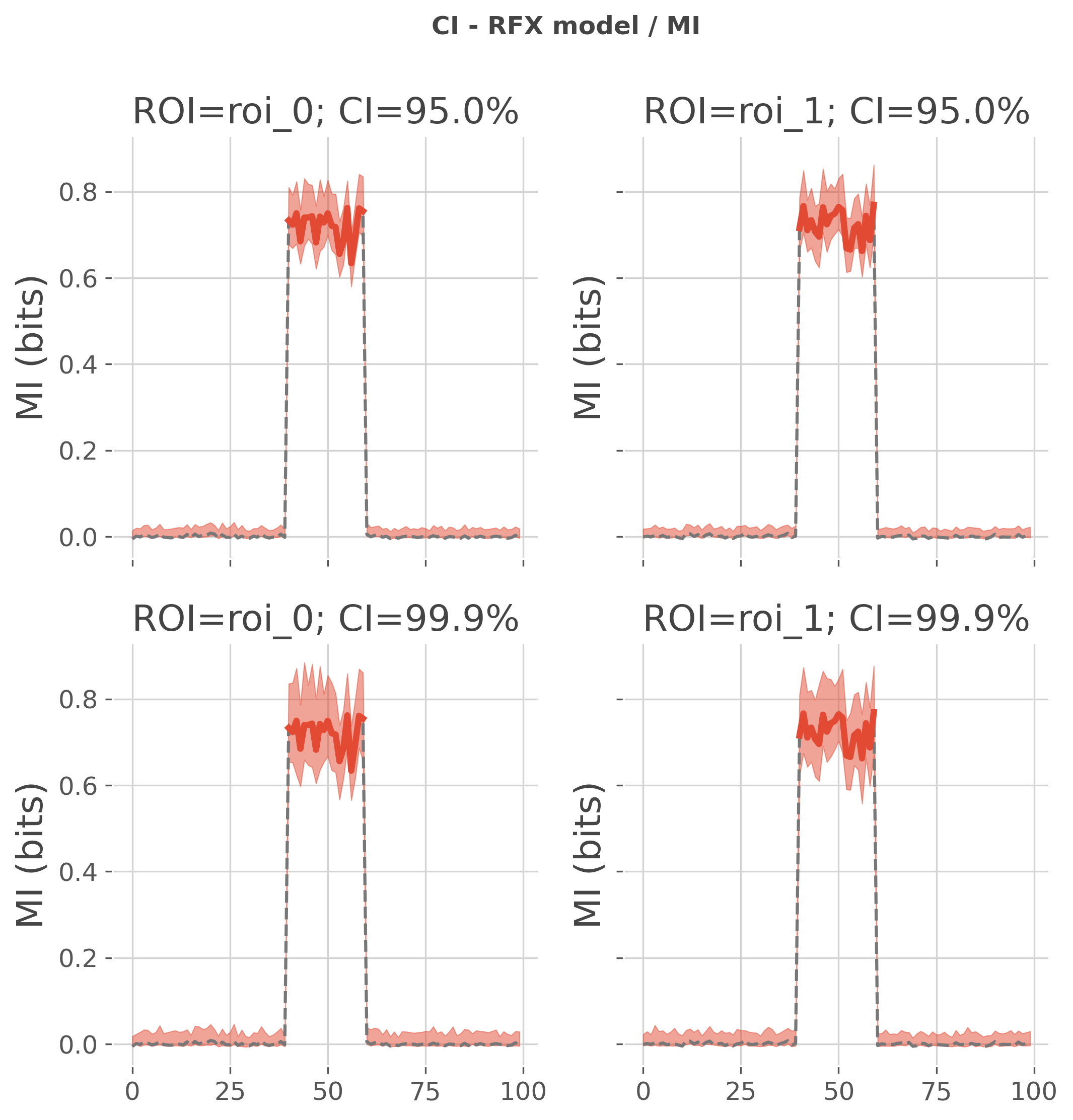
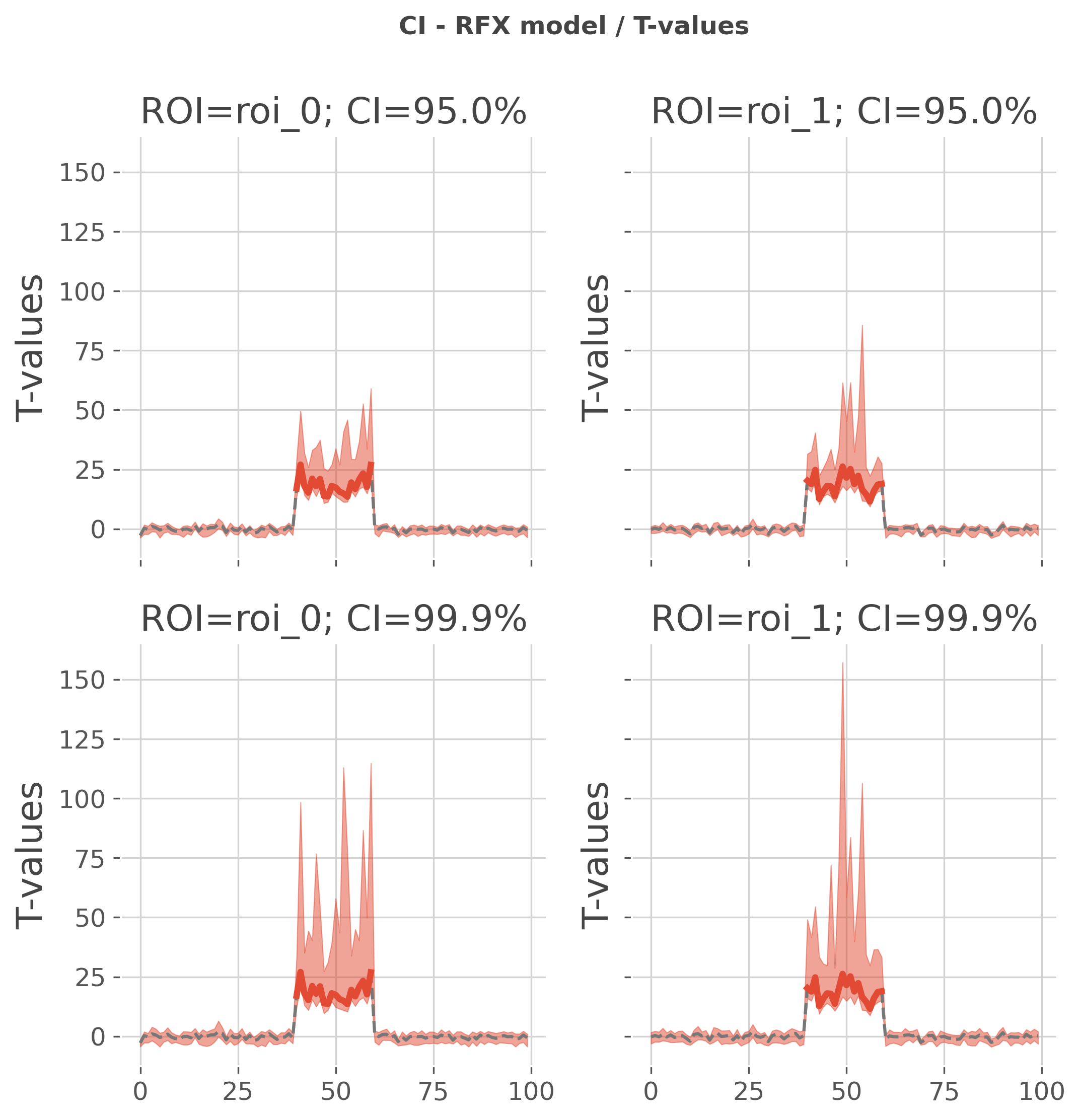
Empirical confidence interval with RFX models#
When using the random-effect model, it’s either possible to estimate the confidence interval on the returned mutual-information or on t-values. To do the switch, you can use the parameter rfx_es for choosing between ‘mi’ or ‘tvalues’
0%| | Estimating MI : 0/2 [00:00<?, ?it/s]
50%|█████ | Estimating MI : 1/2 [00:01<00:01, 1.17s/it]
100%|██████████| Estimating MI : 2/2 [00:02<00:00, 1.16s/it]
100%|██████████| Estimating MI : 2/2 [00:02<00:00, 1.16s/it]
0%| | Estimating CI : 0/2 [00:00<?, ?it/s]
50%|█████ | Estimating CI : 1/2 [00:01<00:01, 1.75s/it]
100%|██████████| Estimating CI : 2/2 [00:03<00:00, 1.75s/it]
100%|██████████| Estimating CI : 2/2 [00:03<00:00, 1.75s/it]
confidence interval on t-values
wf = WfMi(mi_type='cc', inference='rfx')
_, pv = wf.fit(dt, n_perm=200, n_jobs=1, random_state=0)
tv = wf.tvalues
ci = wf.confidence_interval(dt, n_boots=200, ci=[95, 99.9], n_jobs=1,
random_state=0, rfx_es='tvalues')
plot(tv, pv, ci, title='CI - RFX model / T-values', units='T-values')
plt.show()
0%| | Estimating MI : 0/2 [00:00<?, ?it/s]
50%|█████ | Estimating MI : 1/2 [00:01<00:01, 1.15s/it]
100%|██████████| Estimating MI : 2/2 [00:02<00:00, 1.14s/it]
100%|██████████| Estimating MI : 2/2 [00:02<00:00, 1.14s/it]
0%| | Estimating CI : 0/200 [00:00<?, ?it/s]
14%|█▍ | Estimating CI : 28/200 [00:00<00:00, 1715.71it/s]
28%|██▊ | Estimating CI : 56/200 [00:00<00:00, 1721.45it/s]
42%|████▏ | Estimating CI : 83/200 [00:00<00:00, 1703.86it/s]
56%|█████▌ | Estimating CI : 111/200 [00:00<00:00, 1709.12it/s]
70%|██████▉ | Estimating CI : 139/200 [00:00<00:00, 1714.58it/s]
84%|████████▎ | Estimating CI : 167/200 [00:00<00:00, 1718.24it/s]
98%|█████████▊| Estimating CI : 195/200 [00:00<00:00, 1720.42it/s]
100%|██████████| Estimating CI : 200/200 [00:00<00:00, 1648.96it/s]
Total running time of the script: (0 minutes 13.241 seconds)
Estimated memory usage: 83 MB