frites.workflow.WfMi#
- class frites.workflow.WfMi(mi_type='cc', inference='rfx', estimator=None, kernel=None, verbose=None)[source]#
Workflow of local mutual-information and statistics.
This class allows to define a workflow for computing the mutual information and then to evaluate the significance using non-parametric statistics (either within-subjects or between subjects).
- Parameters:
- mi_type{‘cc’, ‘cd’, ‘ccd’}
The type of mutual information that is going to be performed. Use either :
‘cc’ : mutual information between two continuous variables
‘cd’ : mutual information between a continuous and a discret variables
‘ccd’ : mutual information between two continuous variables conditioned by a third discret one
- inference{“ffx”, “rfx”}
Statistical inferences that is desired. Use either :
‘ffx’ : fixed-effect to make inferences only for the population that have been used
‘rfx’ : random-effect to generalize inferences to a random population.
By default, the workflow uses group level inference (‘rfx’)
- estimator
MIEstimator|python:None Estimator of mutual-information. If None, the Gaussian-Copula is used instead.
- kernelnumpy:array_like |
python:None Kernel for smoothing true and permuted MI. For example, use np.hanning(3) for a 3 time points smoothing or np.ones((3)) for a moving average
References
Friston et al., 1996, 1999 [8][9]
- Attributes:
Methods
clean()Clean computations.
confidence_interval(dataset[, ci, n_boots, ...])Estimate the empirical confidence interval.
conjunction_analysis([p, mcp, cluster_th, ...])Perform a conjunction analysis.
copy()Return copy of WfMi instance.
fit([dataset, mcp, n_perm, cluster_th, ...])Run the workflow on a dataset.
get_params(*params[, cis, n_boots, random_state])Get formatted parameters.
- confidence_interval(dataset, ci=95, n_boots=200, rfx_es='mi', n_jobs=-1, random_state=None, verbose=None)[source]#
Estimate the empirical confidence interval.
- Parameters:
- dataset
frites.dataset.DatasetEphy A dataset instance. If the workflow has already been fitted, then this parameter can remains to None.
- ci
python:float,python:list| 95 Confidence level to use in percentage. Use either a single float (e.g. 95, 99 etc.) or a list of floats (e.g. [95, 99])
- n_boots
python:int| 200 Number of resampling to perform
- rfx_es{‘mi’, ‘tvalues’}
For the RFX model, specify whether the confidence interval has to be estimated on a measure of effect size in bits (‘mi’) or on second-level t-test (‘tvalues’)
- n_jobs
python:int| -1 Number of jobs to use for parallel computing (use -1 to use all jobs)
- random_state
python:int|python:None Fix the random state of the machine (use it for reproducibility). If None, a random state is randomly assigned.
- dataset
- Returns:
- ci
xr.DataArray Confidence interval array of shape (n_ci, 2, n_times, n_roi) where n_ci describe the number of confidence levels define with the input parameter ci, and 2 represents the lower and upper bounds of the confidence interval
- ci
Examples using
confidence_interval:
- conjunction_analysis(p=0.05, mcp='cluster', cluster_th=None, cluster_alpha=0.05)[source]#
Perform a conjunction analysis.
This method can be used in order to determine the number of subjects that present a significant effect at a given significiency threshold. Note that in order to work, the workflow of mutual information must have already been launched using the
frites.workflow.WfMi.fit.Warning
In order to work this method require that the workflow has been defined with inference=’rfx’ so that MI are computed per subject
- Parameters:
- p
python:float| 0.05 Significiency threshold to find significant effect per subject.
- kwargs
python:dict| {} Optional arguments are the same as
frites.workflow.WfMi.fitmethod.
- p
- Returns:
- conj_ssnumpy:array_like
DataArray of shape (n_subjects, n_times, n_roi) describing where each subject have significant MI
- conjnumpy:array_like
DataArray of shape (n_times, n_roi) describing the number of subjects that have a significant MI
Examples using
conjunction_analysis: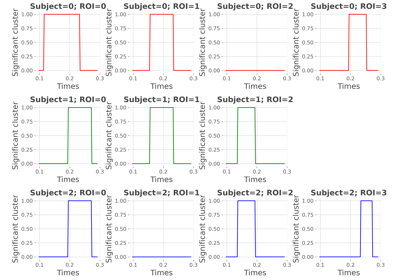
Compute a conjunction analysis on mutual-information
Compute a conjunction analysis on mutual-information
- fit(dataset=None, mcp='cluster', n_perm=1000, cluster_th=None, cluster_alpha=0.05, n_jobs=-1, random_state=None, **kw_stats)[source]#
Run the workflow on a dataset.
In order to run the worflow, you must first provide a dataset instance (see
frites.dataset.DatasetEphy)Warning
When performing statistics at the cluster-level, we only test the cluster size. This means that in your results, you can only discuss about the presence of a significant cluster without being precise about its spatio-temporal properties (see [17])
- Parameters:
- dataset
frites.dataset.DatasetEphy A dataset instance. If the workflow has already been fitted, then this parameter can remains to None.
- mcp{‘cluster’, ‘maxstat’, ‘fdr’, ‘bonferroni’, ‘nostat’,
python:None} Method to use for correcting p-values for the multiple comparison problem. Use either :
‘cluster’ : cluster-based statistics [default]
‘maxstat’ : test-wise maximum statistics correction
‘fdr’ : test-wise FDR correction
‘bonferroni’ : test-wise Bonferroni correction
‘nostat’ : permutations are computed but no statistics are performed
‘noperm’ / None : no permutations are computed
- n_perm
python:int| 1000 Number of permutations to perform in order to estimate the random distribution of mi that can be obtained by chance
- cluster_th
python:str,python:float|python:None The threshold to use for forming clusters. Use either :
a float that is going to act as a threshold
None and the threshold is automatically going to be inferred using the distribution of permutations
‘tfce’ : for Threshold Free Cluster Enhancement
- cluster_alpha
python:float| 0.05 Control the percentile to use for forming the clusters. By default the 95th percentile of the permutations is used.
- n_jobs
python:int| -1 Number of jobs to use for parallel computing (use -1 to use all jobs)
- random_state
python:int|python:None Fix the random state of the machine (use it for reproducibility). If None, a random state is randomly assigned.
- kw_stats
python:dict| {} Additional arguments are sent to
frites.workflow.WfStats.fit
- dataset
- Returns:
- mi, pvaluesnumpy:array_like
DataArray of mutual information and p-values both of shapes (n_times, n_roi). If inference is ‘ffx’ the mi represents the MI computed across subjects while if it is ‘rfx’ it’s the mean across subjects.
References
Maris and Oostenveld, 2007 [13]
Examples using
fit:
Compute a conjunction analysis on mutual-information
Compute a conjunction analysis on mutual-information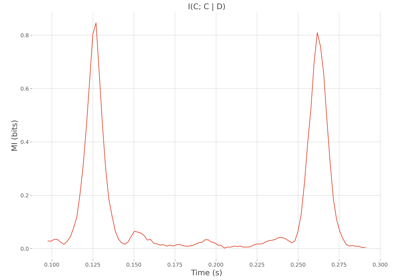
MI between two continuous variables conditioned by a discret one
MI between two continuous variables conditioned by a discret one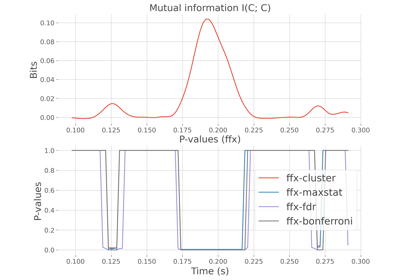
Compare within-subjects statistics when computing mutual information
Compare within-subjects statistics when computing mutual information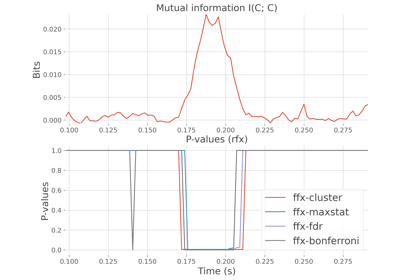
Compare between-subjects statistics when computing mutual information
Compare between-subjects statistics when computing mutual information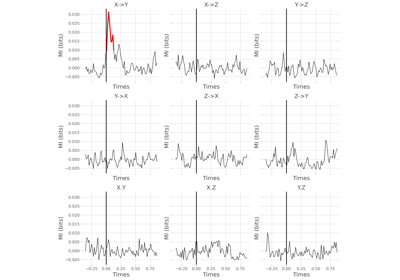
Statistical analysis of a stimulus-specific network
Statistical analysis of a stimulus-specific network
- get_params(*params, cis=95, n_boots=200, random_state=None)[source]#
Get formatted parameters.
This method can be used to get internal arrays formatted as xarray DataArray.
- Parameters:
- params
python:str Internal array names to get as xarray DataArray. You can use :
‘tvalues’ : DataArray of t-values of shape (n_times, n_roi). Only possible with RFX inferences
‘mi_ss’ : DataArray of single subject mutual-information of shape (n_subjects, n_times, n_roi)
‘perm_ss’ : DataArray of computed permutations of shape (n_perm, n_subjects, n_times, n_roi)
‘perm_’ : DataArray of maximum computed permutations of shape (n_perm,)
‘mi_ci’ : DataArray of confidence interval computed when taking the mean of MI across subjects (or sessions). The output shape is (n_ci, 2, n_times, n_roi) where n_ci describe the number of confidence levels define with the input parameter ci, and 2 represents the lower and upper bounds of the confidence interval
- ci
python:float,python:list| 95 Confidence level to use in percentage. Use either a single float (e.g. 95, 99 etc.) or a list of floats (e.g. [95, 99])
- n_boots
python:int| 200 Number of resampling to perform
- random_state
python:int|python:None Fix the random state of the machine (use it for reproducibility). If None, a random state is randomly assigned.
- params
- property mi#
List of length (n_roi) of true mutual information. Each element of this list has a shape of (n_subjects, n_times) if inference is ‘rfx’ (1, n_times) if inference is ‘ffx’.
- property mi_p#
List of length (n_roi) of permuted mutual information. Each element of this list has a shape of (n_perm, n_subjects, n_times) if inference is ‘rfx’ (n_perm, 1, n_times) if inference is ‘ffx’.
- property tvalues#
T-values array of shape (n_times, n_roi) when group level analysis is selected.
- property wf_stats#
Get the workflow of statistics.
Examples using frites.workflow.WfMi#

Compute a conjunction analysis on mutual-information

MI between two continuous variables conditioned by a discret one

Compare within-subjects statistics when computing mutual information

Compare between-subjects statistics when computing mutual information

Statistical analysis of a stimulus-specific network